QM Lecture 3: The Statistical Interpretation

By: Tao Steven Zheng (郑涛)

This article was originally posted on Brilliant.org by the same author.

Figure 1. “Not only does God play dice but... he sometimes throws them where they cannot be seen.” —Stephen Hawking

Probability and Measurement

There are four properties of wavefunctions that we must assume for quantum mechanics to work. The wavefunction $\Psi$ must:

(1) Be square-integrable throughout all space (particles exist and the probability of finding the particle is 100% in the entire space)

$$\int _{ -\infty }^{ \infty }{ { \Psi }^{ * }\Psi } dx =1$$

where ${ \Psi }^{ * }$ is the complex conjugate of $\Psi$. Note that arbitrary wavefunctions can be normalized such that the above equation holds.

(2) Particles can only exist if the wavefunction decays to zero faster than $\frac{1}{\sqrt{|x|}}$ as $x \rightarrow \pm \infty$.

(3) The wavefunction stays normalized as it evolves in time in order for the Schrödinger equation to be continually solved

$$\frac { d }{ dt } \int _{ -\infty }^{ \infty }{ { \Psi }^{ * }\Psi } dx=0.$$

(4) The average is defined to be the expectation value.

If you have encountered statistics before, the above concepts may seem vaguely familiar. Knowledge of probability and statistics is crucial in the study of quantum mechanics because many calculations involve determining significant probabilities and statistical quantities related to the wavefunction. In the orthodox interpretation (more commonly known as the Copenhagen interpretation), the measurable quantity (say the position of a particle) is spread all over space, where in some places there is a higher probability of the particle being there. We can calculate this probability by evaluating the integral of the modulus of the wavefunction ${\Psi}^{*}\Psi$.

Figure 2. Wave and particle nature of matter

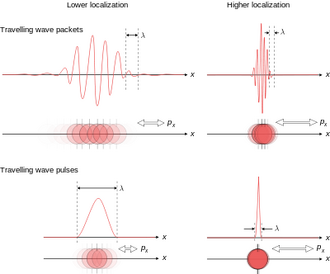
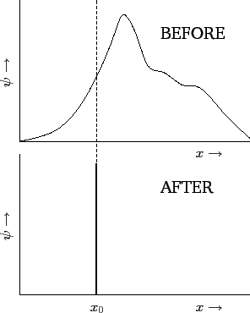
But where is the physics behind this? In the quantum description of the world, a particle can exist everywhere in space at varying degrees of probability as prescribed by its wavefunction. Once we make a measurement of the particle, the particle will lock down on a location by collapsing the wavefunction, producing a sharp peak where the probability becomes 100%. Now, if we immediately measure the particle again, we will discover that the sharp peak stays where it was last measured. However, if we were to stop measuring the particle and give it some time, the sharp peak would gradually spread out.  

Figure 3. Collapse of the wavefunction before and after observation

Expectation values and Observables

Since quantum mechanics is a highly statistical theory of physics, it follows that everything we observe follows statistical rules. Let us begin with two important quantities: position $x$ and momentum $p$. In classical mechanics $x,p$ are just numbers, so this is still true in quantum mechanics but with a twist. In quantum mechanics, we take the expectation of an operator acting on the probability of the wavefunction. For example, the expectation of the position and momentum operators are expressed as

$$\langle\hat{x}\rangle = \int_{-\infty}^{\infty}{\Psi}^{*}\hat{x}{\Psi}dx$$

$$\langle\hat{p}\rangle = \int_{-\infty}^{\infty}{\Psi}^{*}\hat{p}{\Psi}dx.$$

Since the momentum operator is a differential operator of the form

$$\hat{p} =-i\hbar\frac{\partial}{\partial x}$$

then

$$\langle\hat{p}\rangle = \int_{-\infty}^{\infty}{\Psi}^{*}\left(-i\hbar\frac{\partial \Psi}{\partial x} \right) dx.$$

We will accept these expressions for now and study them in more detail later. But first, let us understand why we care about the expectation values of physical quantities. Consider the following scenarios:

(1) In one experiment you make note of $n$ measurements and divide the sum of the measurements by $n$ (average).

(2) You take the average of repeated measurements on $n$ (if best infinite) identically conditioned experiments (expectation value).

From a scientific point of view, which scenario sounds more experimentally sound? Hopefully you chose (2), because that is how science is done. Every experimenter should be able to repeat an experiment and agree that their results corroborate with physical principles. You should think of the expectation value as a stronger average.

Variance and Uncertainty

When we measure the position or momentum of a particle with some wavefunction $\Psi$, we will notice a problem. Although we know the expectation value of said variables, the wavefunction still has some spread $\Delta x = x - \langle x\rangle$ or $\Delta p = p - \langle p \rangle$. Now it is experimentally meaningless to talk about the spread because we will produce useless data if most of the numerical measurements equal the expectation value. Thus, we use the statistical measure called variance ${\sigma}^{2}$ to circumvent this problem. Variance is calculated as the expectation of the square of the spread. For example,

$${{\sigma}_{x}}^{2} = \langle{(\Delta x)}^{2} \rangle = \langle{x}^{2} \rangle - {\langle x \rangle}^{2}.$$

We take the square root of the variance to calculate the standard deviation, which measures the variation of measurable quantities. The standard deviation is convenient for quantum mechanics because we can now discuss the uncertainty of, let's say, the position or momentum of a particle. We will later derive Heisenberg's uncertainty principle (HUP) using operators and Dirac notation (also called bra-ket notation), so for now we shall take a sneak peak of the HUP:

$${\sigma}_{x}{\sigma}_{p} \ge \frac{\hbar}{2}.$$

Problems

Problem 1: Real Eigenenergies

Show that the energy eigenvalues of a wavefunction must be real (as opposed to complex numbers) in order to be normalized for all time $t$.

Hint: Let ${E}_{n} = {E}_{0} + i \Lambda$ for real numbers ${E}_{0}, \Lambda$.

Problem 2: Conservation of Probability

Let the probability density be defined $\rho = {\Psi}^{*}(x,t) \Psi(x,t)$. In quantum mechanics, the probability current is calculated by $J(x,t) = \frac{\hbar}{2mi} \left({\Psi}^{*}\frac{\partial \Psi}{\partial x} - \Psi \frac{\partial {\Psi}^{*}}{\partial x} \right)$.

Use the Schrödinger equation to show that $\frac{\partial \rho}{\partial t} + \frac{\partial J}{\partial x} = 0$. In fact, the conservation of probability extends to three dimensions $\frac{\partial \rho}{\partial t}+\nabla \cdot J=0$.

Solution