Jiuzhang Suanshu Gougu 20

Problem

今有邑方不知大小，各中開門。出北門二十步有木。出南門十四步，折而西行一千七百七十五步見木。問：邑方幾何？ 答曰：二百五十步。 術曰：以出北門步數乘西行步數，倍之，為實。并出南門步數為從法，開方除之，即邑方。

Suppose there is a square city of unknown size with a gate in the middle of each side. Walking from the north gate 20 bu, there is a tree. Walking from the south gate 14 bu, turning west and walking 1775 bu, the tree will just come into view. What is the width of the city? Answer: 250 bu. Method: Multiply the number of bu walked from the north gate by the number of bu walked west, then double this result. Let this be the radicand (實 shi). Add the number of bu walking from the south and north gates, and let this be the (從法 cong fa). Extract the square root to obtain the side of the city.

Solution

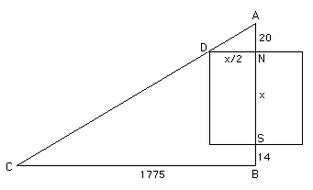
Figure 1. Diagram of the problem

Quadratic Formula Solution

Let $x$ be the width of the town. By proportion,

$$\frac{20}{x/2} = \frac{x+14+20}{1775}.$$

Cross-multiplication and a bit of rearrangement yields the quadratic equation

$${x}^{2} + 34x - 71000 = 0.$$

Use the quadratic equation to solve for $x$.

$$x = \frac{-b \pm \sqrt{{b}^{2} - 4ac}}{2a}$$

$$x = \frac{-34 \pm \sqrt{{34}^{2} - 4(1)(-71500)}}{2(1)}$$

$$x = 250 \quad or \quad x= -284$$

Since the negative root makes no sense for our problem, the width of the square town is 250 bu.

Completing the Square Solution

The ingenious method of the kai fang shu (square root algorithm) was later extended to solve quadratic equations of the form $x^2 + bx = c$, where $x$ is the unknown quantity and $b, c$ are constants. The coefficient of the linear term is called the cong fa (從法), and the Jiuzhang Suanshu does not explicitly explain how the cong fa is incorporated in the square root algorithm. One plausible solution method would be to first implement the well-known technique called "completing the square". By completing the square, one can transform the above quadratic equation into a simpler square root problem. For example, the equation $x^2 + bx = c$ becomes $y^2 = d$ after a change of variable $x = y - \frac{b}{2}$and transformed constant $d = c + {\left(\frac{b}{2}\right)}^{2}$.

After making the transformation $x = y - 17$, the above quadratic equation becomes

$${y}^{2} = 71289$$

Extracting the positive square root gives $y= 267$, which means the final answer is $x=250$. Therefore, the width of the square town is 250 bu.

Horner's Method Solution

The Han dynasty arithmeticians likely solved quadratic equations using the Horner-Ruffini method (nearly two millennia before its discovery in the West). By the Song dynasty (960 - 1279 AD), Chinese mathematicians extended this algorithm to solve polynomial equations up to the tenth degree. Here we express the process algebraically instead of the regular Chinese layout on a counting board.

To solve the above quadratic equation using the Horner-Ruffini method, write it like this

$$x^2 + 34x = 71000.$$

Iteration 1

For the first iteration, the quadratic term should be the dominant term. So search for perfect squares such that $a^2 < 71000 < b^2$.

Notice $200^2 < 71000 < 300^2$. Let $x = y + 200$. Then make the transformation.:

$$(y+200)^2 + 34(y+200) = 71000$$

$$y^2 + 400y + 40000 + 34y + 6800 = 71000$$

$$y^2 + 434y = 24200$$

Iteration 2

For the second iteration, the linear term should be the dominant term. So search for values of $a, b$ such that $434a < 24200 < 434b$.

Notice $434(50) < 24200 < 434(60)$. Let $y = z + 50$. Then make the transformation.

$$(z+50)^2 + 434(z+50) = 24200$$

$$z^2 + 100z + 2500 + 434z + 21700 = 24200$$

$$z^2 + 534z = 0$$

Now this is easy to solve by factoring.

$$z(z + 534) = 0$$

Thus $z=0$ or $z = -534$. Since $x = y + 200$ and $y = z + 50$, it follows that $x = z + 250$. Therefore, $x=250$ or $x = -284$.

You might be wondering why bother going through such a labourious process to solve such a simple quadratic equation? Bear in mind that without the electronic calculator, solving square roots and quadratic equation is quite challenging. So during the Han dynasty, this method would be computationally more efficient than the quadratic formula!